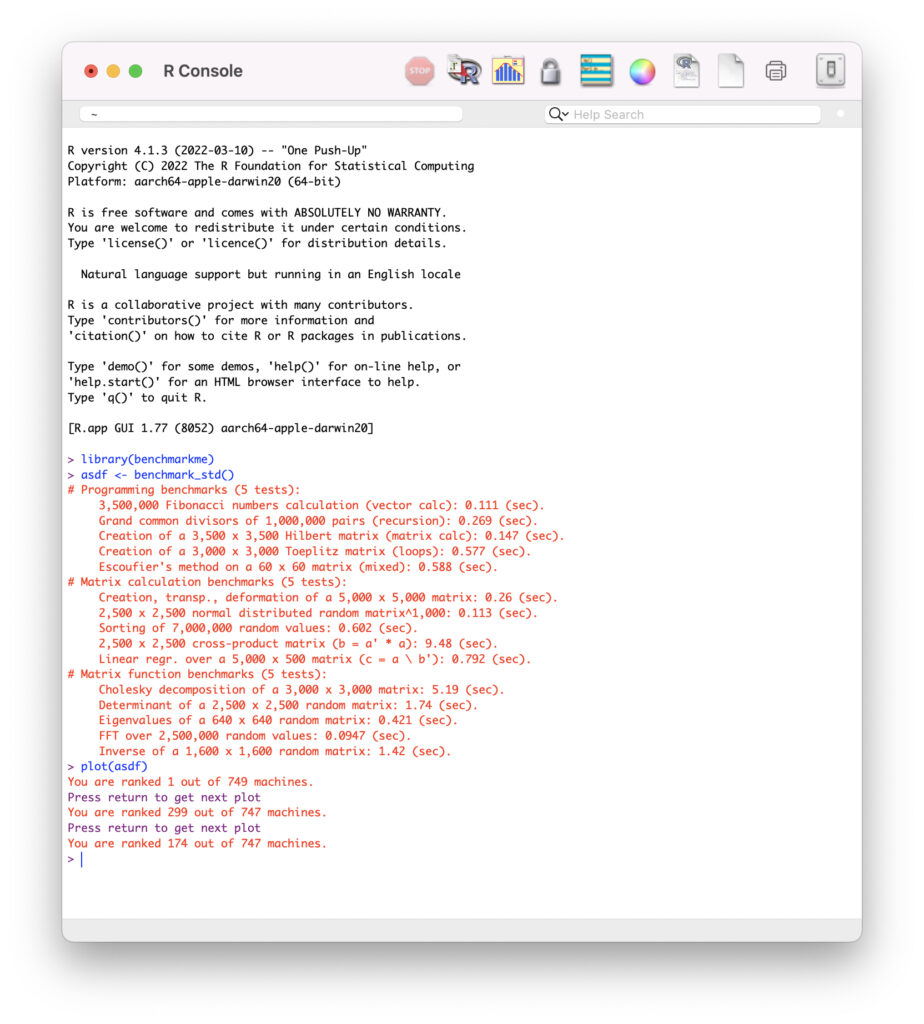
I have a 13″ M1 MacBook Pro with 16 GB memory and 500GB storage. I saw this Reddit posting a few days ago and wondered how mine would perform. I updated R from 4.1.1 to R 4.1.3 binary for macOS 11 (Big Sur) and higher, Apple silicon arm64 build, signed and notarized package. The results were almost similar, although it doesn’t use Rosetta anymore. Anyway, the results are as follows:
R version 4.1.3 (2022-03-10) -- "One Push-Up"
Copyright (C) 2022 The R Foundation for Statistical Computing
Platform: aarch64-apple-darwin20 (64-bit)
R is free software and comes with ABSOLUTELY NO WARRANTY.
You are welcome to redistribute it under certain conditions.
Type 'license()' or 'licence()' for distribution details.
Natural language support but running in an English locale
R is a collaborative project with many contributors.
Type 'contributors()' for more information and
'citation()' on how to cite R or R packages in publications.
Type 'demo()' for some demos, 'help()' for on-line help, or
'help.start()' for an HTML browser interface to help.
Type 'q()' to quit R.
[R.app GUI 1.77 (8052) aarch64-apple-darwin20]
> library(benchmarkme) > asdf <- benchmark_std()
Programming benchmarks (5 tests):
3,500,000 Fibonacci numbers calculation (vector calc): 0.111 (sec). Grand common divisors of 1,000,000 pairs (recursion): 0.269 (sec). Creation of a 3,500 x 3,500 Hilbert matrix (matrix calc): 0.147 (sec). Creation of a 3,000 x 3,000 Toeplitz matrix (loops): 0.577 (sec). Escoufier's method on a 60 x 60 matrix (mixed): 0.588 (sec).
Matrix calculation benchmarks (5 tests):
Creation, transp., deformation of a 5,000 x 5,000 matrix: 0.26 (sec). 2,500 x 2,500 normal distributed random matrix^1,000: 0.113 (sec). Sorting of 7,000,000 random values: 0.602 (sec). 2,500 x 2,500 cross-product matrix (b = a' * a): 9.48 (sec). Linear regr. over a 5,000 x 500 matrix (c = a \ b'): 0.792 (sec).
Matrix function benchmarks (5 tests):
Cholesky decomposition of a 3,000 x 3,000 matrix: 5.19 (sec). Determinant of a 2,500 x 2,500 random matrix: 1.74 (sec). Eigenvalues of a 640 x 640 random matrix: 0.421 (sec). FFT over 2,500,000 random values: 0.0947 (sec). Inverse of a 1,600 x 1,600 random matrix: 1.42 (sec).
> plot(asdf) You are ranked 1 out of 749 machines. Press return to get next plot You are ranked 299 out of 747 machines. Press return to get next plot You are ranked 174 out of 747 machines.